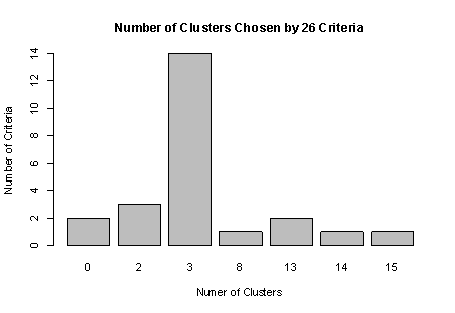
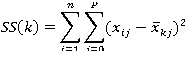In R’s partitioning approach, observations are divided into K groups and reshuffled to form the most cohesive clusters possible according to a given criterion. There are two methods—K-means and partitioning around mediods (PAM). In this article, based on chapter 16 of R in Action, Second Edition, author Rob Kabacoff discusses K-means clustering.
Until Aug 21, 2013, you can buy the book: R in Action, Second Edition with a 44% discount, using the code: “mlria2bl”.
K-means clustering
The most common partitioning method is the K-means cluster analysis. Conceptually, the K-means algorithm:
- Selects K centroids (K rows chosen at random)
- Assigns each data point to its closest centroid
- Recalculates the centroids as the average of all data points in a cluster (i.e., the centroids are p-length mean vectors, where p is the number of variables)
- Assigns data points to their closest centroids
- Continues steps 3 and 4 until the observations are not reassigned or the maximum number of iterations (R uses 10 as a default) is reached.
Implementation details for this approach can vary.
R uses an efficient algorithm by Hartigan and Wong (1979) that partitions the observations into k groups such that the sum of squares of the observations to their assigned cluster centers is a minimum. This means that in steps 2 and 4, each observation is assigned to the cluster with the smallest value of:
Where k is the cluster,xij is the value of the jth variable for the ith observation, and xkj-bar is the mean of the jth variable for the kth cluster.