Guest post by Gergely Daróczi. If you like this content, you can buy the full 396 paged e-book for 5 USD until January 8, 2016 as part of Packt’s “$5 Skill Up Campaign” at https://bit.ly/mastering-R
Feature extraction tends to be one of the most important steps in machine learning and data science projects, so I decided to republish a related short section from my intermediate book on how to analyze data with R. The 9th chapter is dedicated to traditional dimension reduction methods, such as Principal Component Analysis, Factor Analysis and Multidimensional Scaling — from which the below introductory examples will focus on that latter.
Multidimensional Scaling (MDS) is a multivariate statistical technique first used in geography. The main goal of MDS it is to plot multivariate data points in two dimensions, thus revealing the structure of the dataset by visualizing the relative distance of the observations. Multidimensional scaling is used in diverse fields such as attitude study in psychology, sociology or market research.
Although the MASS package provides non-metric methods via the isoMDS function, we will now concentrate on the classical, metric MDS, which is available by calling the cmdscale function bundled with the stats package. Both types of MDS take a distance matrix as the main argument, which can be created from any numeric tabular data by the dist function.
But before such more complex examples, let’s see what MDS can offer for us while working with an already existing distance matrix, like the built-in eurodist dataset:
> as.matrix(eurodist)[1:5, 1:5]
Athens Barcelona Brussels Calais Cherbourg
Athens 0 3313 2963 3175 3339
Barcelona 3313 0 1318 1326 1294
Brussels 2963 1318 0 204 583
Calais 3175 1326 204 0 460
Cherbourg 3339 1294 583 460 0The above subset (first 5-5 values) of the distance matrix represents the travel distance between 21 European cities in kilometers. Running classical MDS on this example returns:
> (mds <- cmdscale(eurodist))
[,1] [,2]
Athens 2290.2747 1798.803
Barcelona -825.3828 546.811
Brussels 59.1833 -367.081
Calais -82.8460 -429.915
Cherbourg -352.4994 -290.908
Cologne 293.6896 -405.312
Copenhagen 681.9315 -1108.645
Geneva -9.4234 240.406
Gibraltar -2048.4491 642.459
Hamburg 561.1090 -773.369
Hook of Holland 164.9218 -549.367
Lisbon -1935.0408 49.125
Lyons -226.4232 187.088
Madrid -1423.3537 305.875
Marseilles -299.4987 388.807
Milan 260.8780 416.674
Munich 587.6757 81.182
Paris -156.8363 -211.139
Rome 709.4133 1109.367
Stockholm 839.4459 -1836.791
Vienna 911.2305 205.930These scores are very similar to two principal components (discussed in the previous, Principal Component Analysis section), such as running prcomp(eurodist)$x[, 1:2]. As a matter of fact, PCA can be considered as the most basic MDS solution.
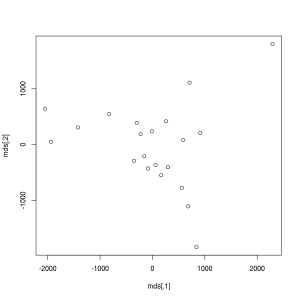
Anyway, we have just transformed (reduced) the 21-dimensional space into 2 dimensions, which can be plotted very easily — unlike the original distance matrix with 21 rows and 21 columns:
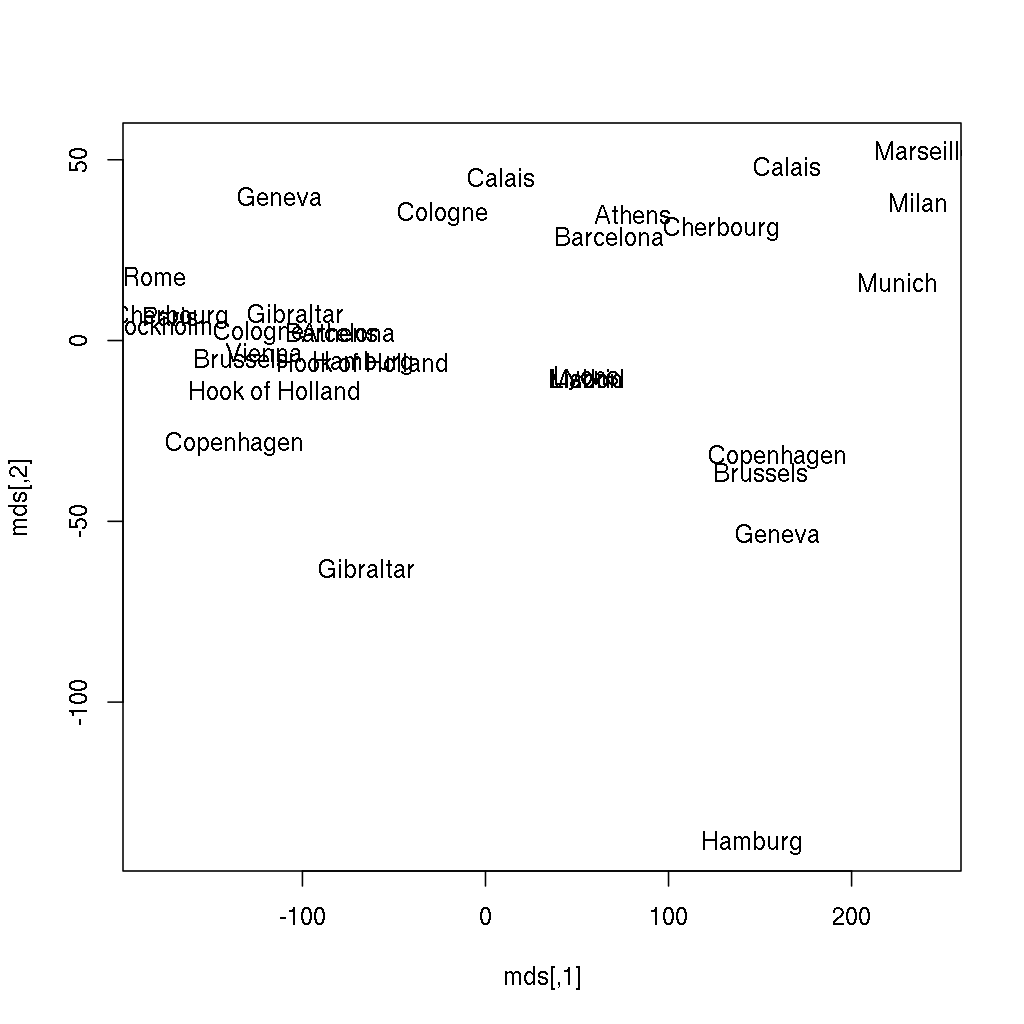
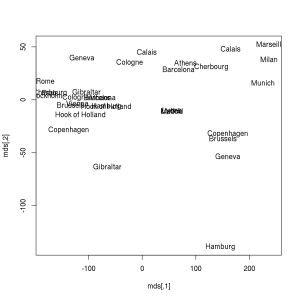
> plot(mds)Does it ring a bell? If not yet, the below image might be more helpful, where the following two lines of code also renders the city names instead of showing anonymous points:
> plot(mds, type = 'n')
> text(mds[, 1], mds[, 2], labels(eurodist))Continue reading “Multidimensional Scaling with R (from “Mastering Data Analysis with R”)”