Post hoc analysis for Friedman’s Test (R code)
February 22nd, 2010 by Tal Galili 
27 Comments My goal in this post is to give an overview of Friedman’s Test and then offer R code to perform post hoc analysis on Friedman’s Test results. (The R function can be downloaded from here)
Preface: What is Friedman’s Test
Friedman test is a non-parametric randomized block analysis of variance. Which is to say it is a non-parametric version of a one way ANOVA with repeated measures. That means that while a simple ANOVA test requires the assumptions of a normal distribution and equal variances (of the residuals), the Friedman test is free from those restriction. The price of this parametric freedom is the loss of power (of Friedman’s test compared to the parametric ANOVa versions).
The hypotheses for the comparison across repeated measures are:
- H0: The distributions (whatever they are) are the same across repeated measures
- H1: The distributions across repeated measures are different
The test statistic for the Friedman’s test is a Chi-square with [(number of repeated measures)-1] degrees of freedom. A detailed explanation of the method for computing the Friedman test is available on Wikipedia.
Performing Friedman’s Test in R is very simple, and is by using the “friedman.test” command.
Post hoc analysis for the Friedman’s Test
Assuming you performed Friedman’s Test and found a significant P value, that means that some of the groups in your data have different distribution from one another, but you don’t (yet) know which. Therefor, our next step will be to try and find out which pairs of our groups are significantly different then each other. But when we have N groups, checking all of their pairs will be to perform [n over 2] comparisons, thus the need to correct for multiple comparisons arise.
The tasks:
Our first task will be to perform a post hoc analysis of our results (using R) – in the hope of finding out which of our groups are responsible that we found that the null hypothesis was rejected. While in the simple case of ANOVA, an R command is readily available (“TukeyHSD”), in the case of friedman’s test (until now) the code to perform the post hoc test was not as easily accessible.
Our second task will be to visualize our results. While in the case of simple ANOVA, a boxplot of each group is sufficient, in the case of a repeated measures – a boxplot approach will be misleading to the viewer. Instead, we will offer two plots: one of parallel coordinates, and the other will be boxplots of the differences between all pairs of groups (in this respect, the post hoc analysis can be thought of as performing paired wilcox.test with correction for multiplicity).
R code for Post hoc analysis for the Friedman’s Test
The analysis will be performed using the function (I wrote) called “friedman.test.with.post.hoc”, based on the packages “coin” and “multcomp”. Just a few words about it’s arguments:
- formu – is a formula object of the shape: Y ~ X | block (where Y is the ordered (numeric) responce, X is a group indicator (factor), and block is the block (or subject) indicator (factor)
- data – is a data frame with columns of Y, X and block (the names could be different, of course, as long as the formula given in “formu” represent that)
- All the other parameters are to allow or suppress plotting of the results.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 | friedman.test.with.post.hoc <- function(formu, data, to.print.friedman = T, to.post.hoc.if.signif = T, to.plot.parallel = T, to.plot.boxplot = T, signif.P = .05, color.blocks.in.cor.plot = T, jitter.Y.in.cor.plot =F) { # formu is a formula of the shape: Y ~ X | block # data is a long data.frame with three columns: [[ Y (numeric), X (factor), block (factor) ]] # Note: This function doesn't handle NA's! In case of NA in Y in one of the blocks, then that entire block should be removed. # Loading needed packages if(!require(coin)) { print("You are missing the package 'coin', we will now try to install it...") install.packages("coin") library(coin) } if(!require(multcomp)) { print("You are missing the package 'multcomp', we will now try to install it...") install.packages("multcomp") library(multcomp) } if(!require(colorspace)) { print("You are missing the package 'colorspace', we will now try to install it...") install.packages("colorspace") library(colorspace) } # get the names out of the formula formu.names <- all.vars(formu) Y.name <- formu.names[1] X.name <- formu.names[2] block.name <- formu.names[3] if(dim(data)[2] >3) data <- data[,c(Y.name,X.name,block.name)] # In case we have a "data" data frame with more then the three columns we need. This code will clean it from them... # Note: the function doesn't handle NA's. In case of NA in one of the block T outcomes, that entire block should be removed. # stopping in case there is NA in the Y vector if(sum(is.na(data[,Y.name])) > 0) stop("Function stopped: This function doesn't handle NA's. In case of NA in Y in one of the blocks, then that entire block should be removed.") # make sure that the number of factors goes with the actual values present in the data: data[,X.name ] <- factor(data[,X.name ]) data[,block.name ] <- factor(data[,block.name ]) number.of.X.levels <- length(levels(data[,X.name ])) if(number.of.X.levels == 2) { warning(paste("'",X.name,"'", "has only two levels. Consider using paired wilcox.test instead of friedman test"))} # making the object that will hold the friedman test and the other. the.sym.test <- symmetry_test(formu, data = data, ### all pairwise comparisons teststat = "max", xtrafo = function(Y.data) { trafo( Y.data, factor_trafo = function(x) { model.matrix(~ x - 1) %*% t(contrMat(table(x), "Tukey")) } ) }, ytrafo = function(Y.data){ trafo(Y.data, numeric_trafo = rank, block = data[,block.name] ) } ) # if(to.print.friedman) { print(the.sym.test) } if(to.post.hoc.if.signif) { if(pvalue(the.sym.test) < signif.P) { # the post hoc test The.post.hoc.P.values <- pvalue(the.sym.test, method = "single-step") # this is the post hoc of the friedman test # plotting if(to.plot.parallel & to.plot.boxplot) par(mfrow = c(1,2)) # if we are plotting two plots, let's make sure we'll be able to see both if(to.plot.parallel) { X.names <- levels(data[, X.name]) X.for.plot <- seq_along(X.names) plot.xlim <- c(.7 , length(X.for.plot)+.3) # adding some spacing from both sides of the plot if(color.blocks.in.cor.plot) { blocks.col <- rainbow_hcl(length(levels(data[,block.name]))) } else { blocks.col <- 1 # black } data2 <- data if(jitter.Y.in.cor.plot) { data2[,Y.name] <- jitter(data2[,Y.name]) par.cor.plot.text <- "Parallel coordinates plot (with Jitter)" } else { par.cor.plot.text <- "Parallel coordinates plot" } # adding a Parallel coordinates plot matplot(as.matrix(reshape(data2, idvar=X.name, timevar=block.name, direction="wide")[,-1]) , type = "l", lty = 1, axes = FALSE, ylab = Y.name, xlim = plot.xlim, col = blocks.col, main = par.cor.plot.text) axis(1, at = X.for.plot , labels = X.names) # plot X axis axis(2) # plot Y axis points(tapply(data[,Y.name], data[,X.name], median) ~ X.for.plot, col = "red",pch = 4, cex = 2, lwd = 5) } if(to.plot.boxplot) { # first we create a function to create a new Y, by substracting different combinations of X levels from each other. subtract.a.from.b <- function(a.b , the.data) { the.data[,a.b[2]] - the.data[,a.b[1]] } temp.wide <- reshape(data, idvar=X.name, timevar=block.name, direction="wide") #[,-1] wide.data <- as.matrix(t(temp.wide[,-1])) colnames(wide.data) <- temp.wide[,1] Y.b.minus.a.combos <- apply(with(data,combn(levels(data[,X.name]), 2)), 2, subtract.a.from.b, the.data =wide.data) names.b.minus.a.combos <- apply(with(data,combn(levels(data[,X.name]), 2)), 2, function(a.b) {paste(a.b[2],a.b[1],sep=" - ")}) the.ylim <- range(Y.b.minus.a.combos) the.ylim[2] <- the.ylim[2] + max(sd(Y.b.minus.a.combos)) # adding some space for the labels is.signif.color <- ifelse(The.post.hoc.P.values < .05 , "green", "grey") boxplot(Y.b.minus.a.combos, names = names.b.minus.a.combos , col = is.signif.color, main = "Boxplots (of the differences)", ylim = the.ylim ) legend("topright", legend = paste(names.b.minus.a.combos, rep(" ; PostHoc P.value:", number.of.X.levels),round(The.post.hoc.P.values,5)) , fill = is.signif.color ) abline(h = 0, col = "blue") } list.to.return <- list(Friedman.Test = the.sym.test, PostHoc.Test = The.post.hoc.P.values) if(to.print.friedman) {print(list.to.return)} return(list.to.return) } else { print("The results where not significant, There is no need for a post hoc test") return(the.sym.test) } } # Original credit (for linking online, to the package that performs the post hoc test) goes to "David Winsemius", see: # http://tolstoy.newcastle.edu.au/R/e8/help/09/10/1416.html } |
Example
(The code for the example is given at the end of the post)
Let’s make up a little story: let’s say we have three types of wine (A, B and C), and we would like to know which one is the best one (in a scale of 1 to 7). We asked 22 friends to taste each of the three wines (in a blind fold fashion), and then to give a grade of 1 till 7 (for example sake, let’s say we asked them to rate the wines 5 times each, and then averaged their results to give a number for a persons preference for each wine. This number which is now an average of several numbers, will not necessarily be an integer).
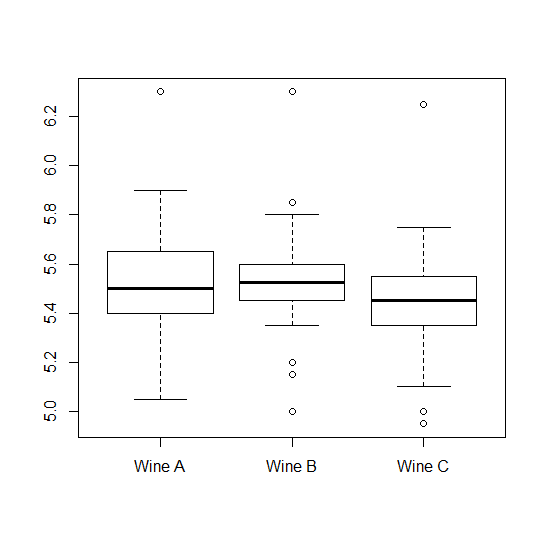
After getting the results, we started by performing a simple boxplot of the ratings each wine got. Here it is:
The plot shows us two things: 1) that the assumption of equal variances here might not hold. 2) That if we are to ignore the “within subjects” data that we have, we have no chance of finding any difference between the wines.
So we move to using the function “friedman.test.with.post.hoc” on our data, and we get the following output:
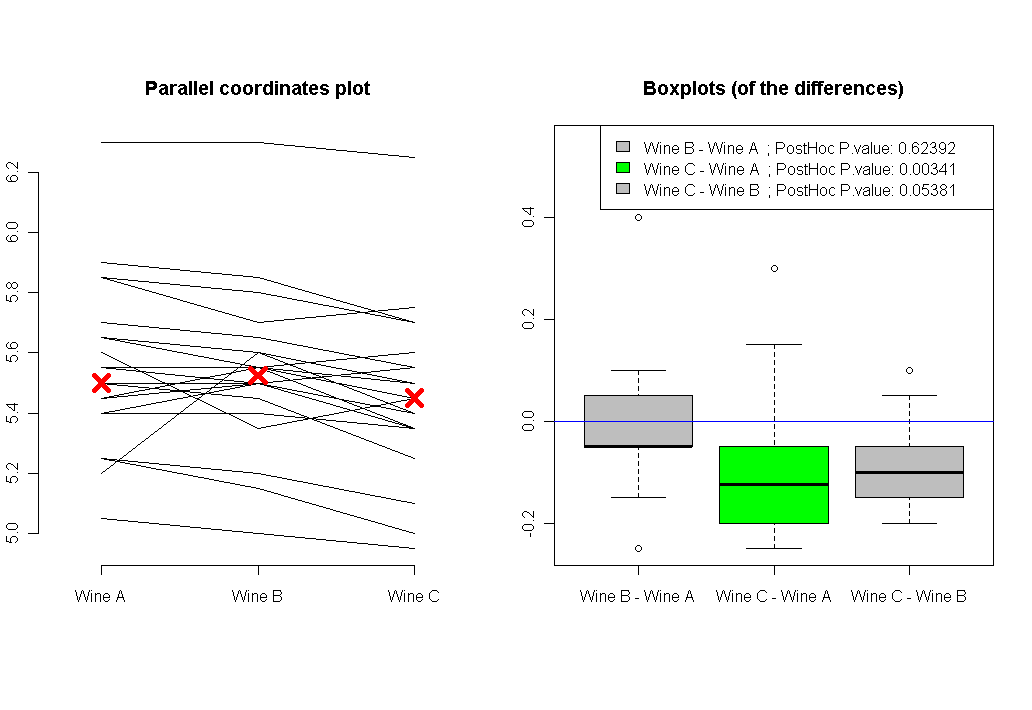
$Friedman.TestAsymptotic General Independence Testdata: Taste byWine (Wine A, Wine B, Wine C)stratified by TastermaxT = 3.2404, p-value = 0.003421$PostHoc.TestWine B – Wine A 0.623935139Wine C – Wine A 0.003325929Wine C – Wine B 0.053772757
The conclusion is that once we take into account the within subject variable, we discover that there is a significant difference between our three wines (significant P value of about 0.0034). And the posthoc analysis shows us that the difference is due to the difference in tastes between Wine C and Wine A (P value 0.003). and maybe also with the difference between Wine C and Wine B (the P value is 0.053, which is just borderline significant).
Plotting our analysis will also show us the direction of the results, and the connected answers of each of our friends answers:
Here is the code for the example:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | source("http://www.r-statistics.com/wp-content/uploads/2010/02/Friedman-Test-with-Post-Hoc.r.txt") # loading the friedman.test.with.post.hoc function from the internet ### Comparison of three Wine ("Wine A", "Wine B", and ### "Wine C") for rounding first base. WineTasting <- data.frame( Taste = c(5.40, 5.50, 5.55, 5.85, 5.70, 5.75, 5.20, 5.60, 5.50, 5.55, 5.50, 5.40, 5.90, 5.85, 5.70, 5.45, 5.55, 5.60, 5.40, 5.40, 5.35, 5.45, 5.50, 5.35, 5.25, 5.15, 5.00, 5.85, 5.80, 5.70, 5.25, 5.20, 5.10, 5.65, 5.55, 5.45, 5.60, 5.35, 5.45, 5.05, 5.00, 4.95, 5.50, 5.50, 5.40, 5.45, 5.55, 5.50, 5.55, 5.55, 5.35, 5.45, 5.50, 5.55, 5.50, 5.45, 5.25, 5.65, 5.60, 5.40, 5.70, 5.65, 5.55, 6.30, 6.30, 6.25), Wine = factor(rep(c("Wine A", "Wine B", "Wine C"), 22)), Taster = factor(rep(1:22, rep(3, 22)))) with(WineTasting , boxplot( Taste ~ Wine )) # boxploting friedman.test.with.post.hoc(Taste ~ Wine | Taster ,WineTasting) # the same with our function. With post hoc, and cool plots |
If you find this code useful, please let me know (in the comments) so I will know there is a point in publishing more such code snippets…
Related posts:
Tags: ANOVA, code, friedman test, friedman's test, multiple comparisons, nonparametric, nonparametric test, one way anova, post hoc, post hoc analysis, posthoc, R, R code, repeated measures, repeated measures anova, test
Posted under: R, statistics
Hi Tal, very interesting post
and definitely worthwhile that you continue posting such snippets.
I am a psychology student currently working on the stats for my MA thesis. I have been using repeated measure ANOVAs to analyze pain perception data. However, some of the normality assumptions are very violated (e.g., extreme skew and kurtosis, many outliers).
I have been thinking of investigating a non-parametric approach to this analysis, and your post has piqued my interest in Friedman’s test.
However, is it possible (excuse my ignorance if this is a stupid question ;P) to incorporate between group analyses in a Friedman’s test? For example, my analysis needs to look like this: 2 (between-group 1:a, b) by 2 (between-group 2: a, b) by 6 (within-group 1: a, b, c, d, e, f)
Further, can Friedman’s test be extended to multivariate repeated measure designs? For example, my potential analyses looks like: 2 (between-group 1:a, b) by 2 (between-group 2: a, b) by 3 (within-group 1: a, b, c) by 6 (within-group 2: a, b, c, d, e, f)
And finally, would your post hoc test be able to extend to these more complex designs? or are there other strategies you would recommend?
Anyways, thanks for the post, it was very interesting
Cheers,
Pat
Hi Pat,
Thank you for your encouraging comment
To your question: The friedman test is about the “between” group (while considering the “within” group). However, it is only one-way (repeated measures) ANOVA. That means that the more sophisticated models you asked about will not be friedman’s test any more.
What you are asking is if it is possible to do multiway non-parametric anova (with/without repeated measures) and with balanced/unbalanced designs – and such that allows you to do posthoc analysis (and if the tests can also be powerful – it would be great). The bad news is that while it might be possible, I don’t have the experience to tell you how.
The good news though, is that there is a generalization of Wilcoxon-Kruskal-Wallis test that can handle interactions in the model. you are worth having a look at the lrm function in the Design package or the polr function in the MASS package. For a tutorial on ordinal logistic regression in ecology (using lrm), see
@Article{gui00ord,
author = {Guisan, Antoine and Harrell, Frank E.},
title = {Ordinal response regression models in
ecology},
journal = {Journal of Vegetation Science},
year = 2000,
volume = 11,
pages = {617-626},
annote = {teaching;ordinal logistic model}
}
(This answer is thanks to the kind answer of Frank Harell, please see here: https://stat.ethz.ch/pipermail/r-help/2008-January/152333.html)
If you get to explore this better and get to find good tutorials/books/insights – please feel welcome to drop by and let me know about them.
All the best,
Tal
Thanks for your helpful reply Tal, I really appreciate your feedback.
I’ll spend some time investigating the the directions you have pointed me and post back any useful new information that I find
Cheers and thanks again Tal,
Pat
———————
note: I had a bit of trouble clicking through that link, but was eventually able to find the post at:
https://mailman.stat.ethz.ch/pipermail/r-help/2008-January/152333.html
Sir, what is the difference between Fishers LSD and Friedman’s Test, How to do Fishers LSD and graph it, thanks for the code, with regards, Samuel, Bangalore India
Hello Dear Duleep,
Regarding Fisher LSD:
Fisher LSD is a post hoc test for ANOVA (which is a parametric test).
Friedman’s test is a type of ANOVA (which is nonparametric one way repeated measures).
The code I presented in this post gives both how to do Friedman’s test AND how to do a post hoc analysis on it.
Doing Fishers LSD means you want to do a post hoc analysis, which relies on a t-test. In a quick search I didn’t find a code for doing it. If you come a cross it, please feel welcome to come back and share the link/code.
All the best,
Tal
Update: I got an e-mail from Duleep Samuel, with an answer to his question.
One can do Fishers LSD with the function “LSD.test” (from the “agricolae” package).
The answer to Samuel came from: Felipe author of Agricolae, Rob author of R in action and Todos Logos.
Hi, Hal.
A very usefull snippet indeed. Particularly liked the boxplot of the differences.
Well done.
Thank you for your very useful code. I was wondering though, (I’m a molecular biologist not a statistician) what is the name of this post hoc analysis? Is it Dunn’s multiple comparison test?
Hi Eric,
The post-hoc tests are:
Wilcoxon-Nemenyi-McDonald-Thompson test
Hollander & Wolfe (1999), page 295
Best,
Tal
Hi Hal,
Like the other posters, i have adopted your code for my own post hoc tests, and ran into a slight bug?
“Error in .local(.Object, …) : ‘x’ is not a balanced factor”
not quite sure to what this is referring… I can send you sample data that produces this error…. do you know what “x” is referring to?
never mind…. missing a data point!
Hi Tal,
Sorry for this question, but I’m not sure of what is the “block” and what is the “group” in my case. Would you be ok to help me?
I have 5 individuals, and a measure for each individual 10 times (“sessions”). I would like to see the effect of sessions apart from effect of individuals.
Anyway thank you for your helpful post.
Sab
Hi Sab,
Thanks for visiting
Your “block” is the 5 individuals, and the “group” is the “sessions”.
Although notice that when doing this for 10 sessions, the resulting plots will be VERY big (all the 10 over 2 permutations = 45 plots).
Consider doing something like merging the different sessions, and checking it on only (for example) quarters of sessions. (If you first looked at the data on how many mergers to make, know that the validity of your choice was a bit shaky, see: http://en.wikipedia.org/wiki/Data_dredging)
Hi, I wonder if it is correct to use the Wilcoxon as a posthoc for Friedman and Mann-Whitney as a posthoc for Kruskall-Wallis?
Tank you!
Anna
Hi Annabel,
That is not what I used in this post, but I believe you can do that. However, you would need to adjust the P values you get (for example, by using the Bonferroni correction).
The advantage of this post hoc method is that it is (probably) more powerful then what you will get using Bonferroni (which can be too conservative sometimes)
Hi Tal,
I was wondering if it’s possible to do a power analysis for Friedman test (i.e., computing the power).
thanks,
Peggy
Hi Peggy.
I don’t know of any existing script that does that. But you could write such a script using bootstaping.
Although you would need to define the structure of your data and then implement the simulation. Not too complex, but takes time and careful thinking.
If you would write such a think, please come back to share.
If you wish to have more help on this, I suggest sending a massage to one of the R mailing lists to see if someone can maybe point to a solution.
Best,
Tal
[...] friedman.test {stats} – Performs a Friedman rank sum test with unreplicated blocked data. That is, a non-parametric one-way repeated measures anova. I also wrote a wrapper function to perform and plot a post-hoc analysis on the friedman test results [...]
Hi.
Regarding question from Pat:
If you have ordinal data from say a likert scale, and you got two groups, how do you analyse these data? In SPSS i cannot see any option to analyse for interaction effects between two groups in Friedmans test. It is all good when you have only 1 group, but with 2 groups it seems as if Friedmans test is useless.
Regards
Hello Jacob,
You are absolutely correct.
The Friedman test is only of use when we are doing a one-way repeated measures (non parametric) ANOVA.
I was wondering myself how this can be performed when the need arise for a multiway ANOVA. As I wrote on my other post repeated measures anova with r (tutorials and functions), I couldn’t (yet) find a solution for this issue. (although there is a solution for multi way, non-parametric, NOT repeated measures, ANOVA. See that post for more on that).
If you ever come about a solution for this case, please let me know.
Best,
Tal
Hi!
Wow, this place has been a huge help to me, thank you, Tal.
I’ve gotten a bit confused though, in my search for the correct statistics for my master thesis in behavioral biology.
I am looking at 10 trainingsessions (over time) with a number of stress related symptoms within each session. These symptoms are a result of a human impact on 10 different animals.
Using the Friedman test I’ve already established that there is a significant difference in the number of symptoms between the 10 sessions. Now I would like to know between which sessions the difference is. Have I understood correctly if I think I can test this with the method mentioned above (the post hoc Friedman)?
Furthermore I would like to make a trendline from session 1 to session 10 showing if the number of symptoms are in- or declining over time. Do you know how to do this in R?
Hope all this makes sence…
Best wishes,
Katrine
Hi Katrine,
I am glad you found my post helpful
If I understood you correctly, your dataset is of 10 animals. For each animal you’ve got 10 (overtime) observation. Each observation is a number (the number of stress factors).
If I got you correctly, then indeed the code in this post (for the post hoc friedman test) could potentially help you.
BUT, I don’t think it will be very helpful.
You are dealing with a case of 10 repeated measures on each individual animal. That means you’ve got 10 over 2 comparisons (45). That is a big number.
Also, you are having a time effect here, why not use it in some way ?
For example, why not only look at 3 time points (start, middle, finish) and make the post hoc comparison on them?
This post hoc might offer more easily interpretable results.
A better yet solution would be to go further and see if you can use some mixed models on your data.
Then, what you are looking to check is if you are having a significant slope for the trend line.
Although I haven’t yet wrote about these methods (and I also don’t know how your data is behaving and how legitimate it is to use mixed models on it).
Consider also giving a look to what I wrote here:
http://www.r-statistics.com/2010/04/repeated-measures-anova-with-r-tutorials/
But if my earlier tip (of just using less data points – to allow interpretation), is not enough for you – then I suggest you try and find some professional help to look at your data and see if mixed models can work on it or not. (Or just learn it by yourself, but it might take some time
)
Regarding the visualization, it is very straight forward.
This tutorial:
http://www.ats.ucla.edu/stat/R/seminars/Repeated_Measures/repeated_measures.htm
Shows how to do it with lattice. You might also want to try ggplot2 for that (both have some learning curve, but offer good results).
Good luck,
Tal
Hi Tal,
Thanks a lot for all your helpfull information.
I have used your code for R to perform a post hoc in a Friedman test. I would like to know how can I cite your code in a journal.
Thanks,
Luis
Hello LuisM,
Thank you very much for offering me the honor of being cited.
Due to my lack of experience, I might be missing on how this should be done, but here is how you might do it:
The analysis was done using R:
@Manual{,
title = {R: A Language and Environment for Statistical
Computing},
author = {{R Development Core Team}},
organization = {R Foundation for Statistical Computing},
address = {Vienna, Austria},
year = 2010,
note = {{ISBN} 3-900051-07-0},
url = {http://www.R-project.org}
}
With the “coin” and “multcomp” packages.
Performing the post-hoc tests of:
Wilcoxon-Nemenyi-McDonald-Thompson test
Hollander & Wolfe (1999), page 295
Using the code of “Tal Galili”, published on r-statistics.com (http://www.r-statistics.com/2010/02/post-hoc-analysis-for-friedmans-test-r-code)
Thanks Tal!!
Hi Tal,
I can’t wait to successfully use the code you have worked out and so kindly shared with us ALL.
To start. i’ve plugged in the following
friedman.test.with.post.hoc <- function(formu, data, to.print.friedman = T, to.post.hoc.if.signif = T, to.plot.parallel = T, to.plot.boxplot = T, signif.P = .05, color.blocks.in.cor.plot = T, jitter.Y.in.cor.plot =F)
I receive a + symbol. Is this correct? I've been working at trying to get my data into your code for 2 days, but am new to R and am struggling.
I have updated the coin, multcomp, and colorspace with success. Does this need to be done in a specific order or each time I reopen R?
I have 3 columns of data. Id = turtle name (block), temperature (factor)…collected stomach temperature from 7 turtles) and time (group)…want to see if there is a difference in stomach temperature for 4 time periods (dawn, day, dusk, night). I do not have 0s or blanks in my data set and found a sig. difference for Friedman.test in R.
any advice would be greatly appreciated!!!
Awesome work. It’s really helping me. I add your blog in my bookmark !